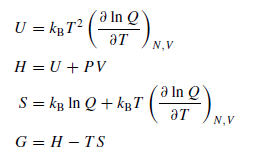Ну да две, например атомы водорода в метане.
Расчёт термодинамических функций молекул
Re: Расчёт термодинамических функций молекул
Не бойтесь будущего, оно не настоящее.
Re: Расчёт термодинамических функций молекул
Про угол C-C-H я не понял, а с этеном действительно, вроде да. Значит для пи-систем нужно вводить какие-то ещё параметры. Могут ли в качестве таких параметров, ну в модели, выступать фиктивные атомы на месте неподелённых электронных пар? Т.е. чтобы этен считался правильно, полагаю стоит добавить четыре фиктивных атома рядом с углеродами, которые тоже отталкиваются и отталкивают другие атомы.Гесс писал(а): ↑Ср авг 09, 2023 2:15 pmТеоретически да, но практически я думаю вы задолбетесь подгонять параметры уже для этана, вам ведь нужно получить не только правильную геометрию но и "квантово-похожий" профиль при малых искажениях. Скажем когда угол C-С-Н отойдет от оптимального. И чем сложнее будет молекула тем ужаснее все будет. Для этилена придется вводить очень большие константы отталкивания, иначе он будет вылетать из плоскости крайне легко.Vit Nhoc писал(а): ↑Ср авг 09, 2023 8:27 amЯ это не понимаю. Разве нужно вводить функционал для углов? Их же много, взаимно зависимых.
Мне казалось, что достаточно ввести функционал для отталкивания между атомами. Например в молекуле этана мы вводим функционал по 7 длинам связей, и плюс к этому отталкивание между всеми парами несвязанных атомов – в результате атомы водорода отталкиваются друг от друга и выстраиваются в (шахматную? В общем D3d) конформацию, в котором двугранный угол H-C-C-H равен 60 градусам. Этого не достаточно?
Не бойтесь будущего, оно не настоящее.
Re: Расчёт термодинамических функций молекул
По сути вы говорите про замену системы координат длины-углы-диэдралы
на систему длины-длины_между_вторыми_соседями-длины_между_третьими_соседями. Причем последние два это чисто расталкивательный потенциал, видимо асимптотический.
Я видел похожую схему для оптимизации помоему в теракеме (как опцию). Но в силовых полях не сталкивался, впрочем повторюсь в третий раз - я не эксперт в силовых полях.
Но давайте посмотрим что нам светит. Попробуем описать исключительно этан, примем в нем все углы тетраэдральными, связь C-C за 1.5А, C-H за 1.0A. Кроме длин связей вы ставите расталкивающие потенциалы, и думаю немного поиграв с их формой и константами расталкивания C...H и H...H вы сможете заставить углы H-C-H и C-C-H быть тетраэрическими. То есть у вас будет силовое поле способное оптимизировать этан в правильную геометрию, отлично, это первый шаг. Но молмех требует от нас еще и правильную энергетику в геометрии недалеко от минимума.
Начнем с простого - колебание связи С-С. То есть мы сделаем релакс-скан на ДФТ или MP2 по длине этой связи от 1.4 до 1.6 с шагом 0.01А и получим что то похожее на параболу. Теперь нам нужно так подкрутить параметры нашего форсфилда чтоб он воспроизвел эту параболу. Компонент по длине связи даст нам прекрасную параболу и им очень легко манипулировать. А вот расталкивающие потенциалы начнут наклонять параболу (сильно задирать ветвь с "короткой" стороны и мало задирать ее с "длинной"). Это впринципе не так плохо, пока этот эффект мал. То есть нам нужно подкрутить параметры так чтобы воспроизводилась эта парабола и при этом попрежнему правильно считалась геометрия. Думаю это всё еще решаемо, особенно если расталкивающий потенциал зависит от расстояния не просто обратно или обратно квадратно, а по какой то 2-3компонентной формуле.
Но мы идем дальше, просканируем угол C-С-H, опять на релевантном методе, опять получим чтото похожее на параболу (пока мы говорим про отклонения скажем до 10 градусов от оптимального 109). Если бы в нащей модели была пружинка описывающая этот угол - мы бы подкрутили ее силовую постоянную и делу конец. Но у нас расталкивающие потенциалы, причем их подкручивание сразу отразится и на оптимальной геометрии и на описании С-C колебания. Вытянем ли мы это? Я не уверен.
А нам еще предстоит описать вращение метилов (то за что в норме отвечает диэдральный угол), причем воспроизвести в первую очередь барьер этого вращения. И это опять упрется в подкручивание расталкивательных потенциалов. Если мы не лопнули до этого момента - тут я думаю мы таки лопнем. И это всего лишь этан. Слишком много взаимодействий завязано на эти расталкивания, и то что в классической схеме рассовано в сравнительно независимые и легко меняемые параметры (углы и диэдральники каждого типа связей) тут надо переоптимизировать совместо.
на систему длины-длины_между_вторыми_соседями-длины_между_третьими_соседями. Причем последние два это чисто расталкивательный потенциал, видимо асимптотический.
Я видел похожую схему для оптимизации помоему в теракеме (как опцию). Но в силовых полях не сталкивался, впрочем повторюсь в третий раз - я не эксперт в силовых полях.
Но давайте посмотрим что нам светит. Попробуем описать исключительно этан, примем в нем все углы тетраэдральными, связь C-C за 1.5А, C-H за 1.0A. Кроме длин связей вы ставите расталкивающие потенциалы, и думаю немного поиграв с их формой и константами расталкивания C...H и H...H вы сможете заставить углы H-C-H и C-C-H быть тетраэрическими. То есть у вас будет силовое поле способное оптимизировать этан в правильную геометрию, отлично, это первый шаг. Но молмех требует от нас еще и правильную энергетику в геометрии недалеко от минимума.
Начнем с простого - колебание связи С-С. То есть мы сделаем релакс-скан на ДФТ или MP2 по длине этой связи от 1.4 до 1.6 с шагом 0.01А и получим что то похожее на параболу. Теперь нам нужно так подкрутить параметры нашего форсфилда чтоб он воспроизвел эту параболу. Компонент по длине связи даст нам прекрасную параболу и им очень легко манипулировать. А вот расталкивающие потенциалы начнут наклонять параболу (сильно задирать ветвь с "короткой" стороны и мало задирать ее с "длинной"). Это впринципе не так плохо, пока этот эффект мал. То есть нам нужно подкрутить параметры так чтобы воспроизводилась эта парабола и при этом попрежнему правильно считалась геометрия. Думаю это всё еще решаемо, особенно если расталкивающий потенциал зависит от расстояния не просто обратно или обратно квадратно, а по какой то 2-3компонентной формуле.
Но мы идем дальше, просканируем угол C-С-H, опять на релевантном методе, опять получим чтото похожее на параболу (пока мы говорим про отклонения скажем до 10 градусов от оптимального 109). Если бы в нащей модели была пружинка описывающая этот угол - мы бы подкрутили ее силовую постоянную и делу конец. Но у нас расталкивающие потенциалы, причем их подкручивание сразу отразится и на оптимальной геометрии и на описании С-C колебания. Вытянем ли мы это? Я не уверен.
А нам еще предстоит описать вращение метилов (то за что в норме отвечает диэдральный угол), причем воспроизвести в первую очередь барьер этого вращения. И это опять упрется в подкручивание расталкивательных потенциалов. Если мы не лопнули до этого момента - тут я думаю мы таки лопнем. И это всего лишь этан. Слишком много взаимодействий завязано на эти расталкивания, и то что в классической схеме рассовано в сравнительно независимые и легко меняемые параметры (углы и диэдральники каждого типа связей) тут надо переоптимизировать совместо.
Re: Расчёт термодинамических функций молекул
А если нужно описать оптимальную геометрию диметилового эфира? Метанола? Воды?Vit Nhoc писал(а): ↑Ср авг 09, 2023 3:39 pmЗначит для пи-систем нужно вводить какие-то ещё параметры. Могут ли в качестве таких параметров, ну в модели, выступать фиктивные атомы на месте неподелённых электронных пар? Т.е. чтобы этен считался правильно, полагаю стоит добавить четыре фиктивных атома рядом с углеродами, которые тоже отталкиваются и отталкивают другие атомы.
Когда начинает изменять память, практики заводят записную книжку, а романтики садятся писать мемуары.
Re: Расчёт термодинамических функций молекул
Если отталкивание между всеми протонами будет одинаковым, то, не принимая во внимание угловые напряжения, получим "перпендикулярный" этан, как на левой картинкеVit Nhoc писал(а): ↑Ср авг 09, 2023 8:27 amНапример в молекуле этана мы вводим функционал по 7 длинам связей, и плюс к этому отталкивание между всеми парами несвязанных атомов – в результате атомы водорода отталкиваются друг от друга и выстраиваются в (шахматную? В общем D3d) конформацию, в котором двугранный угол H-C-C-H равен 60 градусам. Этого не достаточно?
У вас нет необходимых прав для просмотра вложений в этом сообщении.
Re: Расчёт термодинамических функций молекул
У атома кислорода два таких фиктивных атома.Ahha писал(а): ↑Ср авг 09, 2023 11:20 pmА если нужно описать оптимальную геометрию диметилового эфира? Метанола? Воды?Vit Nhoc писал(а): ↑Ср авг 09, 2023 3:39 pmЗначит для пи-систем нужно вводить какие-то ещё параметры. Могут ли в качестве таких параметров, ну в модели, выступать фиктивные атомы на месте неподелённых электронных пар? Т.е. чтобы этен считался правильно, полагаю стоит добавить четыре фиктивных атома рядом с углеродами, которые тоже отталкиваются и отталкивают другие атомы.
Не бойтесь будущего, оно не настоящее.
Re: Расчёт термодинамических функций молекул
Почему? Водороды же будут отталкиваться от водородов и углерода противоположной метильной группы.
Не бойтесь будущего, оно не настоящее.
Re: Расчёт термодинамических функций молекул
Не бойтесь будущего, оно не настоящее.
Re: Расчёт термодинамических функций молекул
Вернусь к исходной теме. Сейчас столкнулся с дурацкой проблемой: сделал в Chemcraft поднятие малых частот до трешолда, а как обосновать что это правильно - не знаю. Помню что где-то читал про этот подход, но не помню где. Подскажите пожалуйста эту информацию.
Я убедился что с этим подходам лучше согласие с экспериментом, но опубликовать статью мне пока не дают. А ещё нашёл статью Prakhta, где он даёт формулу какого-то другого похожего подхода, возможно более обоснованного, наверно надо будет её закодить тоже. Возможно он называется mRRHO или QRRHO, надо выяснить.
Я убедился что с этим подходам лучше согласие с экспериментом, но опубликовать статью мне пока не дают. А ещё нашёл статью Prakhta, где он даёт формулу какого-то другого похожего подхода, возможно более обоснованного, наверно надо будет её закодить тоже. Возможно он называется mRRHO или QRRHO, надо выяснить.
Не бойтесь будущего, оно не настоящее.
Re: Расчёт термодинамических функций молекул
Помню тоже удивился, что теплоемкость мне орка не выдала, выхода нашел два, первый ленивый: просто посчитал для 300К и 301К и разность для внутренней энергии взял, и а второй выход, это колебательную теплоемкость сам считал вставляя значения из орки в производную от энергии колебательных уровней, чуть ли не в экселе(sic!)
У вас нет необходимых прав для просмотра вложений в этом сообщении.
-
some_brero
- Сообщения: 6
- Зарегистрирован: Вс авг 04, 2024 9:20 am
Re: Расчёт термодинамических функций молекул
Тоже считаю вклад колебательных степеней свободы в теплоемкость самостоятельно.
Подскажите, в ORCA можно посчитать энергию возбужденных состояний? На рисунках мои результаты для серы и нескольких молекул. Треугольники соответствуют колебательным частотам, а круги - возбужденным состояниям. Колебательные степени свободы считал сам, а возбужденные состояния брал из справочника. Сравнил с таблицами JANAF.

Подскажите, в ORCA можно посчитать энергию возбужденных состояний? На рисунках мои результаты для серы и нескольких молекул. Треугольники соответствуют колебательным частотам, а круги - возбужденным состояниям. Колебательные степени свободы считал сам, а возбужденные состояния брал из справочника. Сравнил с таблицами JANAF.


Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей и 1 гость